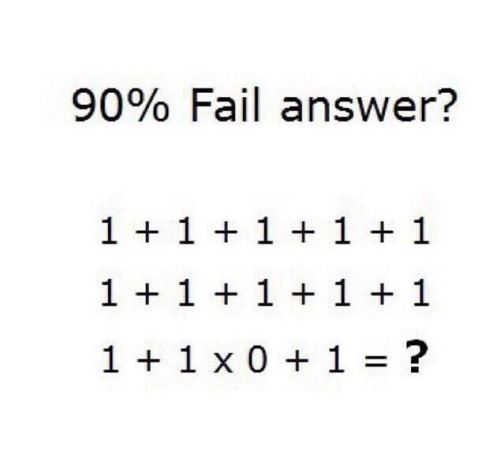182901gzbi8z4oe8e0pbcp.jpg (44.9 KB, 下載次數: 3)
2016-1-5 12:45 上傳
沒錯就是5!
盡管如此,很多網友還是不解地問:“怎麽不是120呢?”,甚至有人問說答案為何是“5”啊?
為何答案是“5!”呢?其實拿起計算機一按,你就會發現“5!”也就是等於120。
182913z0tp8poaxauo88uq.jpg (136.13 KB, 下載次數: 4)
2016-1-5 12:45 上傳
你知道嗎?其實,感嘆號“!”在數學符號上有著階乘的含義(factorial),這也意味著“5!= 5 x 4 x 3 x 2 x 1 = 120”,與 25-55+(85+65) 數出來的答案是一樣的。很多網友看到這正解後,才頓時恍然大悟。但也有網友說:“反正答案就是 120!”
看到這裡,才恍然大悟,原來是被字面上的符號給愚弄了。其實答案是【120】沒錯,只是在數學符號上【!】是階乘的含義,所以【5!】和【120】是一樣的。
「排列」的最直觀意義,就是給定n個「可區別」(Distinguishable,亦作「相 異」)的物件,現把這n個物件的全部或部分排次序,「排列」問題就是求不同排列方式的總數。為了區別這些 物件,我們可不妨給每個物件一個編號:1、2 ... n,因此「排列」問題實際等同於求把數字1、2 ... n的全 部或部分排次序的方式總數。「排列」問題可分為「全排列」和「部分排列」兩種,當我們把給定的n個數字1 、2 ... n全部排次序,求有多少種排法時,就是「全排列」問題。我們可以把排序過程分解為n個程 序:第一個程序決定排於第一位的數字,第二個程序決定排於第二位的數字...第n個程序決定排於第n位的數字 。在進行第一個程序時,有n個數字可供選擇,因此有n種選法。在進行第二個程序時,由於在前一程序已選定 了一個數字,現在可供選擇的數字只剩下n − 1個,因此有n − 1種選法。在進行第三個程序時, 由於在前一程序已選定了一個數字,現在可供選擇的數字只剩下n − 2個,因此有n − 2種選法。 如是者直至第n個程序,這時可供選擇的數字只剩下1個,因此只有1種選擇。由於以上各程序是「各自獨立」的 ,我們可以運用「乘法原理」求得答案為n × (n − 1) × (n − 2) × ... 2 × 1。在數學上把上式簡記為n!,讀作「n階乘」(n-factorial)。
原文: 點算的奧秘:排列和組合基本公式
【免責聲明】
此為網路轉貼及引用文章,純分享非營利。如有侵犯敬請告知,立即刪除。
作者: GFON 時間: 2016-1-5 15:52
本帖最後由 GFON 於 2016-1-5 15:56 編輯
這一題答案是多少呢?
答案如下(反白可看)
1 + 1 + 1 + 1 + 11 + 1 + 1 + 1 + 11 + 1 x 0 + 1=31
就像 4 + 11 + 3 + 11 + 0 + 1 => 30
作者: ranth 時間: 2016-1-5 17:34
本帖最後由 ranth 於 2016-1-5 17:35 編輯
我是90%裡的一份子
那個11分段,擺明“坑爹”啊~~~~

作者: infd555 時間: 2016-1-5 23:09
我太笨不能理解

作者: abn0911 時間: 2016-1-6 02:34
這跟我們的法律一樣擺明是玩文字遊戲.真是吭爹啊.考試出這種題目是要人怎麼過關啊
作者: willam654 時間: 2016-1-9 23:37
本帖最後由 willam654 於 2016-1-9 23:39 編輯
25-55+(85+65)=
25-55+150=
-30+150=
120
120=5!
| 歡迎光臨 Android 台灣中文網 (https://apk.tw/) | Powered by Discuz! X3.1 |